1. Coherence X Mac
2. Coherence Pro App

Estimate the magnitude squared coherence estimate, Cxy, ofdiscrete-time signals X and Y using Welch’s method.

Cxy=abs(Pxy)**2/(Pxx*Pyy), where Pxx and Pyy are powerspectral density estimates of X and Y, and Pxy is the crossspectral density estimate of X and Y.

View 2.pptx from CS 5420 at Cornell University. Cache Coherence x x P1 x x P3 Pn P2 -Multiple copies of x -What if P1 updates. Coherence X allows you to turn websites into powerful chromium-based apps on your Mac. Use Chrome extensions, profiles, and more.

Time series of measurement values

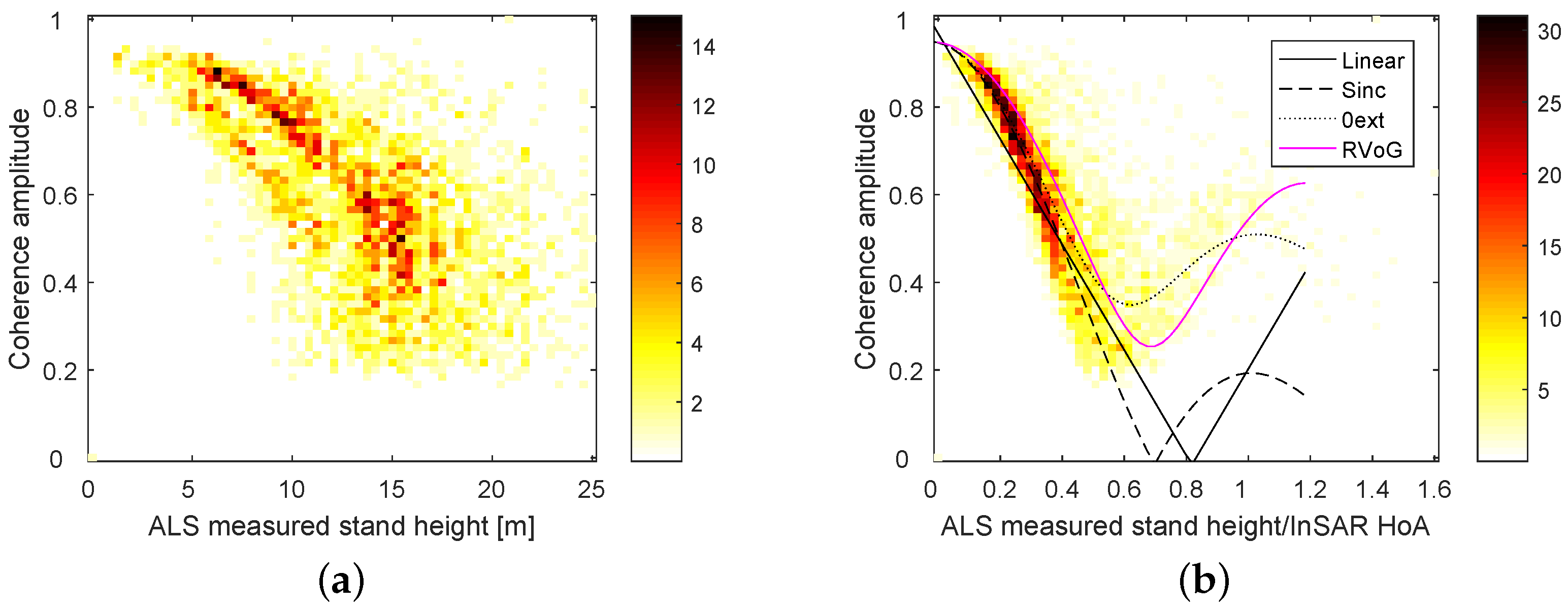
Time series of measurement values

Sampling frequency of the x and y time series. Defaultsto 1.0.

Desired window to use. If window is a string or tuple, it ispassed to get_window to generate the window values, which areDFT-even by default. See get_window for a list of windows andrequired parameters. If window is array_like it will be useddirectly as the window and its length must be nperseg. Defaultsto a Hann window.

Length of each segment. Defaults to None, but if window is str ortuple, is set to 256, and if window is array_like, is set to thelength of the window.

Number of points to overlap between segments. If None,noverlap=nperseg//2. Defaults to None.

Length of the FFT used, if a zero padded FFT is desired. IfNone, the FFT length is nperseg. Defaults to None.

Specifies how to detrend each segment. If detrend is astring, it is passed as the type argument to the detrendfunction. If it is a function, it takes a segment and returns adetrended segment. If detrend is False, no detrending isdone. Defaults to ‘constant’.

Axis along which the coherence is computed for both inputs; thedefault is over the last axis (i.e. axis=-1).

Array of sample frequencies.

Magnitude squared coherence of x and y.

See also

Simple, optionally modified periodogram

Lomb-Scargle periodogram for unevenly sampled data

Power spectral density by Welch’s method.

Cross spectral density by Welch’s method.

Notes

An appropriate amount of overlap will depend on the choice of windowand on your requirements. For the default Hann window an overlap of50% is a reasonable trade off between accurately estimating thesignal power, while not over counting any of the data. Narrowerwindows may require a larger overlap.

References

P. Welch, “The use of the fast Fourier transform for theestimation of power spectra: A method based on time averagingover short, modified periodograms”, IEEE Trans. AudioElectroacoust. vol. 15, pp. 70-73, 1967.

Coherence X Mac

Stoica, Petre, and Randolph Moses, “Spectral Analysis ofSignals” Prentice Hall, 2005

Examples

Generate two test signals with some common features.

Maurice steger vivaldi photo. Compute and plot the coherence.

Coherence Pro App

In physics, coherence length is the propagation distance over which a coherent wave (e.g. an electromagnetic wave) maintains a specified degree of coherence. Wave interference is strong when the paths taken by all of the interfering waves differ by less than the coherence length. A wave with a longer coherence length is closer to a perfect sinusoidal wave. System requirements for mac os 9. Coherence length is important in holography and telecommunications engineering.

This article focuses on the coherence of classical electromagnetic fields. In quantum mechanics, there is a mathematically analogous concept of the quantum coherence length of a wave function.

Formulas[edit]

In radio-band systems, the coherence length is approximated by

${\displaystyle L=\frac{c}{n\mathrm{\Delta }f}=\frac{{\lambda }^2}{n\mathrm{\Delta }\lambda },}$

where ${\displaystyle c}$ is the speed of light in a vacuum, ${\displaystyle n}$ is the refractive index of the medium, and ${\displaystyle \mathrm{\Delta }f}$ is the bandwidth of the source or ${\displaystyle \lambda }$ is the signal wavelength and ${\displaystyle \mathrm{\Delta }\lambda }$ is the width of the range of wavelengths in the signal.

In optical communications, assuming that the source has a Gaussian emission spectrum, the coherence length ${\displaystyle L}$ is given by ^[1]

${\displaystyle L=\frac{1}{2}{L}_{FWHM}=\frac{2\ln 2}{\pi }\frac{{\lambda }^2}{n\mathrm{\Delta }\lambda },}$

where ${\displaystyle \lambda }$ is the central wavelength of the source, ${\displaystyle n}$ is the refractive index of the medium, and ${\displaystyle \mathrm{\Delta }\lambda }$ is the (FWHM) spectral width of the source. If the source has a Gaussian spectrum with FWHM spectral width ${\displaystyle \mathrm{\Delta }\lambda }$, then a path offset of ±${\displaystyle L}$ will reduce the fringe visibility to 50%.

Coherence length is usually applied to the optical regime.

The expression above is a frequently used approximation. Due to ambiguities in the definition of spectral width of a source, however, the following definition of coherence length has been suggested:

The coherence length can be measured using a Michelson interferometer and is the optical path length difference of a self-interfering laser beam which corresponds to a ${\displaystyle 1/e=37\mathrm{\%}}$ fringe visibility,^[2] where the fringe visibility is defined as

${\displaystyle V=\frac{I_{max}-I_{min}}{I_{max}+I_{min}},}$

where ${\displaystyle I}$ is the fringe intensity.

Serial number for adobe photoshop cc mac. In long-distance transmission systems, the coherence length may be reduced by propagation factors such as dispersion, scattering, and diffraction.

Lasers[edit]

Multimode helium–neon lasers have a typical coherence length of 20 cm, while the coherence length of single-mode lasers can exceed 100 m. Semiconductor lasers reach some 100 m, but small, inexpensive semiconductor lasers have shorter lengths, with one source^[3] claiming 20 cm. Singlemode fiber lasers with linewidths of a few kHz can have coherence lengths exceeding 100 km. Similar coherence lengths can be reached with optical frequency combs due to the narrow linewidth of each tooth. Non-zero visibility is present only for short intervals of pulses repeated after cavity length distances up to this long coherence length.

Other light sources[edit]

Tolansky's 'An introduction to Interferometry' has a chapter on Sources which quotes a line width of around 0.052 Angstroms for each of the Sodium D lines in an uncooled low-pressure sodium lamp, corresponding to a coherence length of around 67 mm for each line by itself. Cooling the low pressure sodium discharge to liquid nitrogen temperatures increases the individual D line coherence length by a factor of 6. A very narrow-band interference filter would be required to isolate an individual D line.

See also[edit]

References[edit]

1. ^Akcay, C.; Parrein, P.; Rolland, J.P. (2002). 'Estimation of longitudinal resolution in optical coherence imaging'. Applied Optics. 41 (25): 5256–5262. doi:10.1364/ao.41.005256. PMID12211551. equation 8
2. ^Ackermann, Gerhard K. (2007). Holography: A Practical Approach. Wiley-VCH. ISBN978-3-527-40663-0.
3. ^'Sam's Laser FAQ - Diode Lasers'. www.repairfaq.org. Retrieved 2017-02-06.

• This article incorporates public domain material from the General Services Administration document: 'Federal Standard 1037C'. (in support of MIL-STD-188)